Hybrid DSP Core
Current multimedia applications involve three main transforms: DCT for image transformation and video processing, DFT is a core component in signal processing and communication devices while the DWT based on Haar matrix has been extensively used in applications involving sharp signal changes like fingerprint recognition, handwriting detection etc. In order to combine these powerful transforms on the same platform, researchers have introduced a new hybrid transformation model based on matrix decomposition to identify the common sub-matrices among these transforms. The project ultimately aims to exploit this common features of the transforms to design a pipelined hybrid reconfigurable architecture for implementing 1D 8 point transforms using two level hardware mapping and ultimately synthesize on a FPGA board to study its efficiency in terms of latency, area utilized, power consumed.
Matrix Decomposition
[Ho Lee, 2000] presents a fast source coding algorithm for representation of DFT/DCT/Wavelet Transforms on a single hybrid model. It uses element wise inverse matrix factorization algorithm to decompose the coefficient matrices of all the three transforms in to an orthogonal matrix and a special sparse matrix.
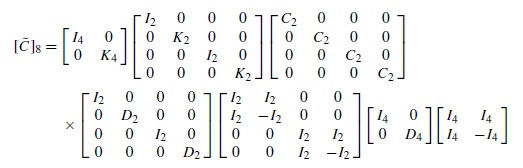
Decomposed submatrix of DCT

Decomposed submatrix of DFT
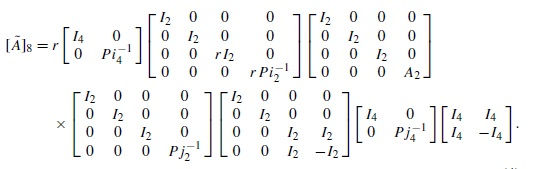
Decomposed submatrix of DWT
Hybrid Core Architecture


High-Level description of the core (left) and Finite-State machine for control flow (right) (courtesy of [Wahid et. al. 2009])
The hybrid architecture implemented by this project contains the submodules which function together to enable the
user to continuously feed 8 point 1D coefficients into the model and generating the transformed coefficients.The hybrid architecture contains the following core modules:
1. Input Coefficients: They contain several datasets of 8 8bit coefficients for further processing according to the
transformation selected by the user.
2. Delay lines: The model contains two two delay lines, one each at input and output to latch in and out the data and to
give sufficient delays between transform operations.
3. Controller: Handles important signals and states of the processor for transform operations.
4. Transform Modules: Core modules based on the decomposition algorithm to implement the transformation operation
on the inputs received.
5. Output Coefficients: They arrive in a parallel manner to the output delay lines. They contain two sets of data, real
and imaginary, each with a size of 8 bits.
Transform Submodules
The transform submodules play the major role in the processor. These blocks have been designed based on the decomposed sub-matrices using Chen and lee’s algorithm. While some of the modules have been designed using the butterfly flow graphs presented in [Ho Lee, 2000], design of custom transform modules were also done apart from the other
existing ones in order to accommodate wide range of data input and also for supporting our floating point multiplier units. The transforms are divided into many modules, each of them might include one or more sub-matrix components of the three transforms.
The modules are named according to their sub-matrix components involved and the stage in the pipeline at which they are called. For eg. the module CFH 6 indicates that all the three transform components are involved in that core and is called at the 6th stage. The core modules contain many other sub components such as Adders, subtractors,multipliers, shifters etc. to calculate the incoming real coefficients. Our project contains a total of 22 modules including the transform modules in order to implement the desired transform operation and generate the output coefficients. For instance, CFH 6 includes all the three transform components and is called at stage 6 while CF 2 includes only the DCT and DFT while being calledat stage 2. The number of inputs taken by each module depends on the operation performed by them. After each operation in a stage, the outputs of these modules will be forwarded to the modules
called in the next stage.
Apart from the main modules mentioned above, the core modules transform the input coefficients received with the help of other sub modules such as the following:
(a) Adders: capable of handling sign-extended addition of 12-bit numbers. (sign-encoding used)
(b) Subtractors: capable of handling sign-extended subtraction of 12-bit numbers. (similar-encoding used
(c) Multiplier: capable of handling sign-extended and fixed-point multiplication of data items and transform coefficients. The input to the multiplier is taken in as a 32 bit signed value. Based on our custom encoding, we have assigned the 31st bit
for signed bit.
(d) Shifters: Left Shifter and Right Shifters are frequently used wherever possible to substitute sign-extended multiplication. [Coefficients r squared and 1/r squared ].
Based on the matrix decomposition algorithm, we have identified that it was more efficient to add multiple shifters to incorporate the above coefficients rather than
sending them to multipliers directly.
Synthesized Hybrid Core
Results
1. In terms of Hardware demand, the DCT-DFT, popular standalone core reports suggest a gate count of minimum 34000. Our gate count for entire core is 24340.
2. Considering, in the worst case that HWT takes up only 20% of the gates it gives us 19472 gates for the DCT-DFT subprocessor.
3. This is 42.5% improvement in hardware resources.
4. The minimum clock period should be about 16ns. This means the Frequency is at least 62.5 MHz.
5. A popular DCT (8X8 1D) found in literature has a frequency of 20 MHz and since DCT is the most critical of the three transforms, it can be safely assumed that an improvement of over 200% in any one will not be less than 20% improvement
hen considering the other two transforms. (We were targeting a minimum 20% improvement in performance)
References
Moon Ho Lee, ”A New Reverse Jacket Transform and Its Fast Algorithm,” IEEE, Trans. on Circuit and System, vol. 47. no. 1, pp.39-47, Jan. 2000.
K. Wahid, S. Shimu, M. Islam, D. Teng, M. Lee, S.-B. Ko, Efficient hardware implementation of hybrid cosine-Fourier-wavelet transforms on a single FPGA, in Proc. of the IEEE International Symposium on Circuits and Systems (2009), pp. 23252328
For codes, a detailed report and more, visit my github repository here

